정규분포(Normal distribution)는 연속확률분포(즉, 정수 뿐만아니라 연속된 값을 취할 수 있는 분포)의 하나로, 가우스 분포(Gaussian distribution)라고도 한다.
정규분포는 일상적인 자료에서 흔히 볼 수 있는 분포이다.
가령 전체 부서 남자 직원의 키를 조사했을 때 보통 평균값 주변에 많이 분포되어 있고, 평균 값에서 멀어질수록 더 적은 수가 분포되어 있는 것을 생각해보면 된다.
특히 모집단의 수가 클 경우 정규분포를 근사적으로 따를 것으로 가정하고 통계적 분석을 할 수 있다.
그러나 이 외에도 정규분포가 통계학에서 아주 유용하게 사용되는 이유는 따로 있다.
중심극한정리(Central limit theorem, CLT)가 바로 그 것인데, 간단히 설명하자면 모든 표본 평균의 분포가 표본의 크기가 커짐에 따라 정규분포에 유사한 형태로 변해간다는 정리이다.
1. 정규분포의 특성
1) 분포는 좌우 대칭의 형태를 띠며, 평균치에서 확률값이 가장 높다.
2) 곡선 아래의 전체 면적은 1이다.
3) 곡선은 평균으로부터 멀어질수록 x축에 가까워지나, 결코 x축에 닿지 않는다.
즉, 확률 값은 절대 0을 가지지 않는다.
4) 정규분포는 평균과 분산 값에 따라 다른 형태를 띤다.
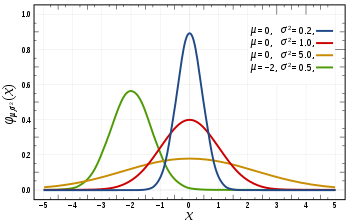
위 그림은 각기 다른 평균값과 분산을 가지는 4개의 정규분포 그래프를 보여준다.
1)을 보자. 평균을 기준으로 좌우대칭을 이루고 있고, 평균치에서 값이 가장 높은 최고점을 이루는 것을 볼 수 있다.
2) 모든 곡선의 넓이는 1이다. 그 이유는 모든 확률 값의 합은 1이기 때문이다.
3) 그래프는 모두 0에 닿을만큼 가까워보이지만, 이는 축척때문에 마치 0인 것처럼 보이는 것이고 사실은 0.00001과 같은 아주 작은 값을 띠고 있다.
4)각 각 평균과 분산 값에 따라 달리 분포하고 있는 것을 알 수 있다.
파랑,빨강,노랑 그래프는 모두 평균이 0으로, 분산 값만 각자 다르다.
분산이 클수록 넓게 분포해 있기 때문에 x축에 달라 붙은 모양을 띠고, 반대로 분산이 작을수록 평균값인 0에 가까이 분포해 있는 것을 알 수 있다.
특히, 빨강 그래프는 평균 0, 분산 1을 갖는 표준정규분포그래프이다.
녹색 그래프는 홀로 평균이 -2이기때문에 좌측으로 평행이동한 형태를 띤다.
<확률 밀도 함수>
모수가 ( μ , σ2 ) 인 정규분포의 확률밀도함수는 다음과 같다.
( σ > 0 )
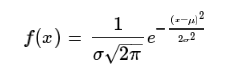
이 분포는 다음과 같이 표현한다.
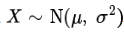
'정보처리기술사' 카테고리의 다른 글
| 메타휴리스틱스 - [126화 1교시] (0) | 2022.03.01 |
|---|