벡터:
벡터의 덧셈: 두 벡터를 더하려면 양쪽 벡터의 각 성분을 더해야 한다.
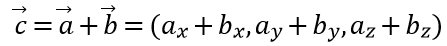

벡터의 뺄셈: 벡터에서 벡터를 빼려면 다음과 같이 두 벡터의 각 성분을 빼야 한다.
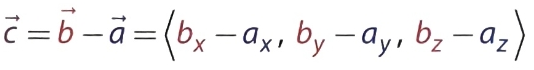
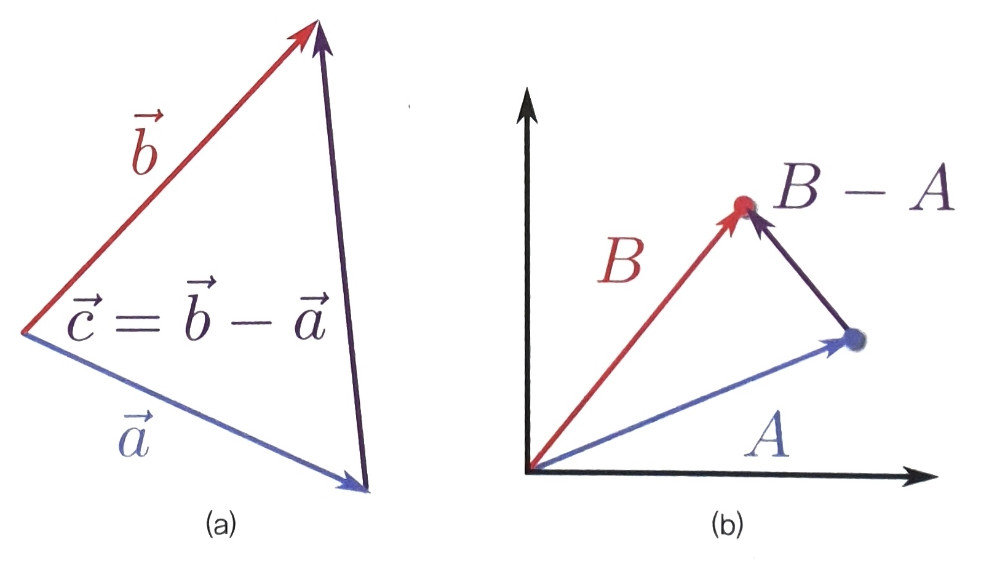
두 점을 잇는 벡터를 만들 수 있다는 뺄셈의 특징은 게임 내에서 빈번하게 쓰인다. 예를 들어 화살표로 방향을 지시하는 UI를 만들어야 할 때 화살표의 방향은 플레이어의 위치에서 목적지를 잇는 벡터의 방향과 같아야 하며 다음과 같이 계산할 수 있다.
arrowVector = objective.position - player.position
벡터의 길이: 벡터의 길이를 계산하는 공식은 다음과 같다.
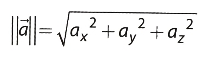
흔히 거리를 구하는 공식과 동일하며, 실제로 원점과 벡터가 가리키는 위치 사이의 거리를 계산하는 공식이다.
두 객체간 거리를 정확하게 구해야 한다면 공식처럼 제급근을 구해야 하지만, 단순히 거리 비교라면 연산cost가 큰 제곱근을 구할 필요없이 양쪽을 제곱한 상태로 비교하자.
벡터의 길이를 알면 단위 벡터(unit vector)를 구할 수 있다. 단위 벡터란 길이가 1인 벡터를 말한다.
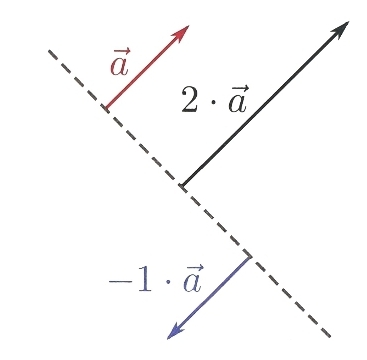
스칼라 곱: 벡터에 스칼라를 곱하려면 다음과 같이 각 성분에 스칼라를 곱해야 한다.
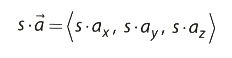
내적: 벡터를 마치 수처럼 곱하는 방식으로 내적의 결과로 스칼라가 나오고, 두 벡터가 이루는 각도를 찾는 용도로 많이 쓰인다.
벡터에는 방향이 있으므로, 방향이 일치하는 만큼만 곱한다. 예를 들어 두 벡터의 방향이 같으면, 두 벡터의 크기를 그냥 곱한다. 두 벡터가 이루는 각이 90도일 땐, 일치하는 정도가 전혀 없기 때문에 내적의 값은 0이다. 내적은 한 벡터를 다른 벡터로 정사영 시켜서, 그 벡터의 크기를 곱한다.

하지만 곱셈식에는 각도에 관한 내용이 없다.
두 벡터가 이루는 각을구하려면 다음과 같이 삼각법에 의해 내적을 구하는 공식을 사용해야 한다.
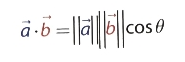
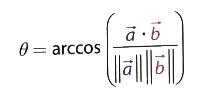
아래 그림처럼 벡터 a와 b가 모두 단위 벡터라면 길이가 모두 1이므로 부모를 생략할 수 있다. 방향에만 관심이 있는 벡터를 미리 정규화해 놓아야 하는 이유 중 하나가 바로 이런 식으로 공식을 간소화할 수 있기 때문이다.

두 단위 벡터의 내적이 0이면 서로 직각을 이루는 벡터다. (cos90 = 0)
두 단위 벡터의 내적이 1이면 서로 평행을 이루는 벡터다.
두 단위 벡터의 내적이 -1이면 서로 평행한 채 방향이 반대인 벡터다.

다음 그림과 같이 스칼라 투영도 내적의 중요한 특성이다. 그림에서는 단위 벡터(a)와 단위 벡터가 아닌 벡터(b)를 사용했는데, 단위 벡터를 늘려서 다른 벡터와 직각 삼각형을 만들었을 때, 늘어난 단위 벡터의 길이가 내적의 결과가 된다.
그 밖의 유용한 특성은 길이의 제곱이 벡터 자신의 내적과 같다는 점이다.
벡터의 반사: 벡터를 사용해서 반사를 계산해내면 벽의 방향에 상관없이 모든 반사 문제를 계산할 수 있다.

v의 꼬리에서 v'의 머미로 이어지는 벡터를 안다면